Den enkle harmoniske bevegelsen ble oppfunnet av den franske matematikeren Baron Jean Baptiste Joseph Fourier i 1822. Edwin Armstrong (18. DEC 1890 til 1. FEBRUAR 1954) observerte svingninger i 1992 i sine eksperimenter og Alexander Meissner (14. SEP 1883 til 3. JAN 1958) oppfant oscillatorer i mars 1993. Begrepet harmonisk er et latinsk ord. Denne artikkelen diskuterer en oversikt over den harmoniske oscillatoren som inkluderer definisjon, type og applikasjoner.

Hva er Harmonic Oscillator?

Harmonisk oscillator er definert som en bevegelse der kraften er direkte proporsjonal med partikkelen fra likevektspunktet og den produserer utgang i en sinusformet bølgeform. Kraften som forårsaker harmonisk bevegelse kan matematisk uttrykkes som

F = -Kx

Hvor,

F = Gjenopprettingskraft

K = Fjærkonstant

X = avstand fra likevekt

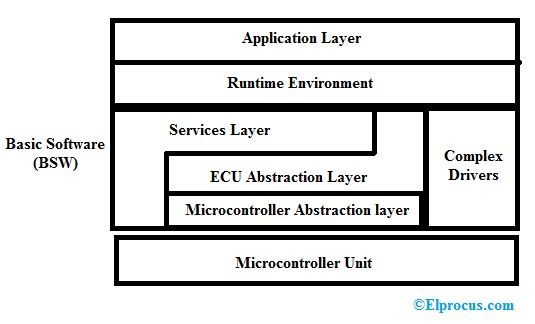
blokkdiagram-av-harmonisk-oscillator

Det er et punkt i harmonisk bevegelse der systemet svinger, og kraften som bringer massen igjen og igjen på samme punkt fra hvor den starter, kalles kraften gjenopprettingskraft og punktet kalles likevektspunkt eller middelposisjon. Denne oscillatoren er også kjent som en lineær harmonisk oscillator . Energien strømmer fra aktiv komponenter til passive komponenter i oscillatoren.

Blokkdiagram

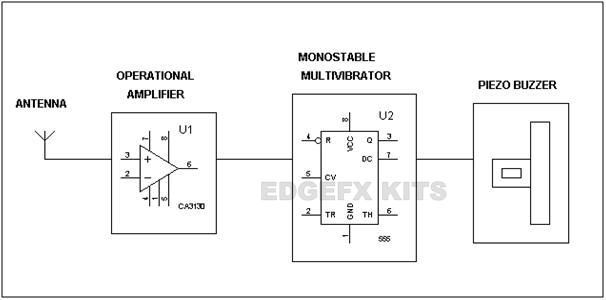
De blokkdiagram over den harmoniske oscillatoren inneholder en forsterker og et tilbakemeldingsnettverk. Forsterkeren brukes til å forsterke signalene og at forsterkede signaler sendes gjennom et tilbakemeldingsnettverk og genererer utgangen. Der Vi er inngangsspenningen, Vo er utgangsspenningen og Vf er tilbakemeldingsspenningen.

Eksempel

Mass på en vår: Fjæren gir gjenopprettingskraft som akselererer massen og gjenopprettingskraften uttrykkes som

F = ma

Hvor ‘m’ er massen og a er en akselerasjon.

“hva er hensikten med et sim -kort ”

mass-on-a-spring

Våren består av en masse (m) og kraft (F). Når kraften trekker massen på et punkt x = 0 og bare avhenger av x - massens posisjon og fjærkonstanten er representert med bokstaven k.

Typer harmonisk oscillator

Typer av denne oscillatoren inkluderer hovedsakelig følgende.

Tvungen harmonisk oscillator

Når vi bruker ekstern kraft på systemets bevegelse, sies det at bevegelsen er en tvungen harmonisk oscillator.

Damped Harmonic Oscillator

Denne oscillatoren er definert som når vi bruker ekstern kraft på systemet, reduseres oscillatorens bevegelse og dens bevegelse sies å være dempet harmonisk bevegelse. Det er tre typer dempet harmoniske oscillatorer de er

demping-bølgeformer

Overdempet

Når systemet beveger seg sakte mot likevektspunktet, sies det å være en overdampet harmonisk oscillator.

Under Damped

Når systemet beveger seg raskt mot likevektspunktet, sies det å være en overdampet harmonisk oscillator.

Kritisk dempet

Når systemet beveger seg raskt som mulig uten å svinge rundt likevektspunktet, sies det å være en overdampet harmonisk oscillator.

Kvantum

Den er oppfunnet av Max Born, Werner Heisenberg og Wolfgang Pauli ved “University of Göttingen”. Ordet kvante er det latinske ordet og betydningen av kvante er en liten mengde energi.

Zero Point Energy

Nullpunktsenergien er også kjent som bakkenergi. Det er definert når jordtilstandsenergi alltid er større enn null, og dette konseptet blir oppdaget av Max Planck i Tyskland og formelen utviklet i 1990.

Gjennomsnittlig energi av dempet enkel harmonisk oscillatorligning

Det er to typer energier, de er kinetisk energi og potensiell energi. Summen av kinetisk energi og potensiell energi er lik den totale energien.

E = K + U ………………. Likestilling (1)

Hvor E = Total energi

K = Kinetisk energi

U = Potensiell energi

Hvor k = k = 1/2 mv^to………… ekv. (2)

U = 1/2 kx^to………… ekv. (3)

oscillasjonssyklus- for gjennomsnittlige verdier

Gjennomsnittsverdiene for kinetisk og potensiell energi per oscillasjonssyklus er lik

Hvor v^to= v^to(TIL^to-x^to) ……. ekv. (4)

Erstatning eq (4) i eq (2) og eq (3) vil få

k = 1/2 m [w^to(TIL^to-x^to)]

= 1/2 m [Aw cos (wt + ø₀)]^to……. likestilling (5)

U = 1/2 kx^to

= 1/2 k [A sin (wt + ø₀)]^to……. ekv. (6)

Erstatning eq (5) og eq (6) i eq (1) vil få den totale energiværdien

E = 1/2 m [b^to(TIL^to-x^to)] + 1/2 kx^to

= 1/2 m v^to-1/2 m v^toTIL^to+ 1/2 kx^to

= 1/2 m v^toTIL^to+1/2 x^to(K-mw^to) ……. ekv. (7)

Hvor mw^to= K , erstatt denne verdien i ekv. (7)

E = 1/2 K A^to- 1/2 Kx^to+ 1/2 x^to= 1/2 K A^to

Total energi (E) = 1/2 K A^to

Gjennomsnittlig energi for en tidsperiode uttrykkes som

TIL_gj.sn.= U_gj.sn.= 1/2 (1/2 K A^to)

Harmonisk oscillatorbølgefunksjon

Hamilton-operatøren uttrykkes som en sum av kinetisk energi og potensiell energi, og den uttrykkes som

ђ (Q) = T + V ………………. ekv. (1)

Hvor ђ = hamitonske operatør

T = Kinetisk energi

V = Potensiell energi

For å generere bølgefunksjonen må vi kjenne Schrodinger-ligningen og ligningen uttrykkes som

-đ^to/ 2μ * d^toѱ_υ(Q) / dQ^to+ 1 / 2KQ^toѱ_υ(Q) = E._υѱ_υ(Q) …………. likestilling (2)

Hvor Q = Normal koordinatlengde

Μ = Effektiv masse

K = Kraftkonstant

Schrodinger-ligningsgrensebetingelser er:

Ѱ (-∞) = ø

Ѱ (+ ∞) = 0

Vi kan også skrive eq (2) som

d^toѱ_υ(Q) / dQ^to+ 2μ / đ^to(E_υ-K / 2 * Q^to) ѱ_υ(Q) = 0 ………… ekv. (3)

Parametere som brukes til å løse en ligning er

β = ђ / √μk ……… .. ekv. (4)

d^to/ dQ^to= 1 / β^tod^to/ dx^to………… .. ekv. (5)

Erstatt eq (4) og eq (5) i eq (3), så blir differensiallikningen for denne oscillatoren

d^toѱ_υ(Q) / dx^to+ (2μb^toE_υ/ đ^to- x^to) ѱ_υ(x) = 0 ……… .. ekv. (6)

Det generelle uttrykket for maktserier er

ΣC¬nx2 …………. ekv. (7)

En eksponentiell funksjon uttrykkes som

exp (-x^to/ 2) ………… ekv. (8)

eq (7) multipliseres med eq (8)

ѱυ (x) = ΣC¬nx2exp (-x2 / 2) …………… ..eq (9)

Hermite-polynomer oppnås ved å bruke ligningen nedenfor

ђ_υ(x) = (-1)^υ* exp (x^to) d / dx^υ* exp (-x^to) …………… .. ekv. (10)

Normaliseringskonstanten uttrykkes som

N_υ= (1/2^υυ! √Π)^1/2…………… .ekv (11)

De enkel harmonisk oscillatorløsning uttrykkes som

Ѱ_υ(x) = N_υH_υ(og) e^{-x2 / 2}……………… ekvivalenter (12)

Hvor N_υer normaliseringskonstanten

H _υer eremitten

er ^{-x2 / to}er gausseren

En ligning (12) er bølgefunksjonen til den harmoniske oscillatoren.

Denne tabellen viser den første termen Hermite polynomer for de laveste energitilstandene

^υ	0	1	to	3
H_υ(Y)	1	2y	4y^to-2	8 år³-12 år

Bølgefunksjonene til enkel harmonisk oscillatorgraf for fire laveste energitilstander er vist i figurene nedenfor.

bølgefunksjoner-av-harmonisk-oscillator

Sannsynlighetstettheten til denne oscillatoren for de fire laveste energitilstandene er vist i figurene nedenfor.

sannsynlighet-tettheter-av-bølgeformer

applikasjoner

Simple harmonisk oscillatorapplikasjoner inkluderer hovedsakelig følgende

Audio- og videosystemer
Radio og andre kommunikasjonsenheter
Omformere , Alarmer
Summere
Dekorative lys

Fordeler

De fordelene med den harmoniske oscillatoren er

Billig
Høyfrekvent generasjon
Høy effektivitet
Billig
Bærbar
Økonomisk

Eksempler

Eksemplet på denne oscillatoren inkluderer følgende.

Musikkinstrumenter
Enkel pendel
Massefjærsystem
Svinge
Bevegelsen til klokka
Bevegelsen til hjulene på bilen, lastebilen, bussen osv

Det er en type bevegelse som vi kan observere på våre daglige baser. Harmonisk oscillator bølgefunksjon ved bruk av Schrodinger og ligninger av den harmoniske oscillatoren er avledet. Her er et spørsmål, hvilken type bevegelse utført av strikkhopping?